En el artículo anterior, se contextualizó la importancia que tiene el estudio del frente de onda y las aberraciones en la calidad visual humana. En esta sección se presentará el abordaje matemático del estudio de las aberraciones ópticas. En términos cuantitativos, es necesario traer a colación la variable RMS, que se entiende como la raíz cuadrada media de la deformación del frente de onda, que básicamente es la raíz cuadrada de la varianza del frente de onda. Se establece que la RMS es igual a 0 en un caso ideal donde no existe varianza del frente de onda y, por lo tanto, el sistema óptico estaría libre de aberraciones. Cuando esta variable toma un valor positivo, se asume la presencia de un frente de onda aberrado.1 Los datos derivados de los frentes de onda se descomponen en forma de suma lineal de términos, gracias a los polinomios de Zernike, revelando así el error cuadrático medio total (RMS), para interpretar en un solo valor el compendio de las características de los frentes de onda de la superficie óptica. Por esta razón, se ha determinado que la combinación de las funciones independientes de Zernike es ideal para la representación de superficies complejas, al reducirlas a coordenadas polares (r, θ), con lo que se desprende la siguiente ecuación:
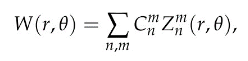
En la configuración de esta ecuación, el coeficiente Cnm es proporcional al peso de una aberración Zernike específica que esté presente en el sistema óptico. El subíndice n se conoce como el orden radial y está siempre representado por valores positivos. Para el caso del superíndice m, éste representa la frecuencia angular y puede estar determinado en valores tanto positivos como negativos. Con base en lo anterior, se construye la pirámide de Zernike, que representa una forma útil para describir de forma ordinal el sistema de polinomios de Zernike.1,2
Al observar esta pirámide, cuando se analizan los datos aberrométricos de ojos normales y anormales, el coeficiente de orden radial 0 que se denomina “pistón”, así como el coeficiente de orden radial 1, llamados “tip” y “tilt” generalmente se ignoran porque se refieren solo a un cambio de fase o a un desplazamiento de imagen respectivamente, y no a su calidad. Por otro lado, el orden radial 2 se relaciona con aberraciones de desenfoque y astigmatismo, también se describe que algunos ordenes radiales 3 y 4 se relacionan con aberración esférica primaria, (Z_4^0) y aberraciones en coma ( Z_3^{-1} para un coma vertical y Z_3^1 para un coma horizontal). Ver Figura 1.
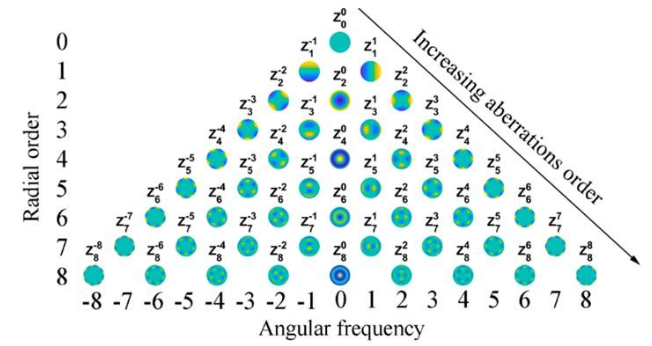
Al incrementarse el orden radial, va avanzando hacia aberraciones de mayor orden, las cuales se caracterizan por tener una forma y terminología más compleja (tetrafoil, pentafoil, hexafoil), los enfoques de análisis de la imagen a través de métricas del plano-imagen, se usan para describir el efecto de la aberración óptica sobre la calidad de la imagen. Una de las métricas más usadas es la función de dispersión de puntos (PSF, por su sigla en inglés), la cual representa la calidad de la imagen al observar objetos puntuales. Otra métrica utilizada es la función de transferencia óptica (OTF, por su sigla en inglés), que es usada para objetos tipo rejilla. Las siguientes ecuaciones representan la PSF, que corresponde al módulo al cuadrado de la transformada de Fourier de la función pupilar P(x,y), donde A(x,y) corresponde a la distribución de amplitud, y W(x,y) es la deformación del frente de onda en la pupila analizada.1,3
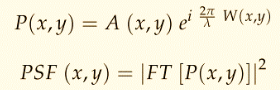
La siguiente ecuación, está determinada para la OTF, que se obtiene mediante la inversa de la transformada de Fourier de la función de dispersión puntual (PSF).
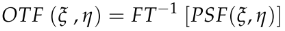
Las métricas del plano de la imagen representan una descripción del error del frente de onda al incidir sobre la retina. De esta forma, las aberraciones pueden afectar la imagen de una rejilla reduciendo el contraste o desplazando la imagen lateralmente alterando la fase de percepción espacial. Los cambios que se presentan en la frecuencia espacial del contraste de la imagen, así como el cambio de fase respectivamente, se describen mediante la función de transferencia de modulación (MTF, por su sigla en inglés) y la función de transferencia de fase (PTF, por su sigla en inglés), que se expresan por la contribución real e imaginaria de la OTF, llamadas por lo tanto módulo y fase de OTF. Las anteriores variables se representan a través de las siguientes ecuaciones:1
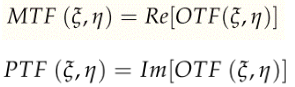
Con este contexto, se abre la puerta para incluir el estudio aberrométrico en diferentes situaciones que afectan la calidad visual y se generen estrategias reducir las aberraciones y preservar la calidad de la imagen. La aplicación en la salud visual, por lo tanto, representa un análisis más profundo de las superficies ópticas.
REFERENCIAS
1. Vacalebre M, Frison R, Corsaro C, Neri F, Conoci S, Anastasi E, et al. Advanced Optical Wavefront Technologies to Improve Patient Quality of Vision and Meet Clinical Requests. Polymers (Basel). 2022;14(23).
2. Tomas J. Aberrometría ocular : aplicaciones clínicas y limitaciones de los sensores de frente de onda. Cienc Tecnol para la Salud Vis y Ocul. 2014;12(2014):93–105.
3. Olarte RV. Entendiendo e interpretando las aberraciones ópticas understanding and Interpreting Optical Aberrations. Cien Tecnol Salud Vis Ocul [Internet]. 2011;9(2):105–22. Available from: www.dorronsoro.net






De los artículos que más me ha gustado!, creo que las ciencias visuales del futuro van a tener como base la física pura como ciencia primaria; gracias a estas ecuaciones y experimentos que las confirman, el desarrollo tecnológico de manejo ocular cada día es más increíble, no más miremos como a partir de una ecuación podemos diseñar lentes Esclerales personalizados y ligar esos datos a un software inteligente para crear impresiones únicas que cambian vidas; definitivamente entender estas ecuaciones en aberrometría nos abre un campo de estudio importante porque entre mejor entendamos su comportamiento en el ojo, seremos capaces de crear mejores soluciones para su corrección.
Saludos!.