La óptica ha dado un giro inesperado. En el horizonte de la Optometría se avista una incontenible etapa de evolución, no solo en el terreno de la refracción sino en todas sus áreas clínicas. En el interior de los metamateriales la luz se desplaza a mayor velocidad que los electrones. El sector energético, las telecomunicaciones, las ciencias básicas, las sociales y una larga lista de disciplinas pronto se verán sacudidas por el ocaso de la electrónica y la eclosión de la era fotónica.1
La diferencia entre la velocidad de la luz en el vacío y su velocidad en un medio se conoce como índice de refracción (n) y siempre adquiere un valor positivo. Mientras más densa la composición de la materia, mayor cantidad de átomos contiene, mayor su índice de refracción y menor su velocidad (Ver Figura 1).2
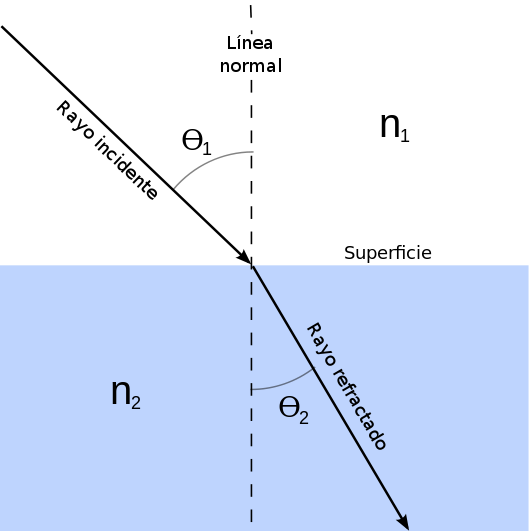
Figura 1. Un rayo de luz que pasa desde un medio con determinada densidad a otro de mayor densidad modifica su trayectoria aproximándose a la línea normal perpendicular a la superficie y disminuye su velocidad en función de su constante dieléctrica (Ɛ) y su permeabilidad magnética (µ). Imagen tomada de: https://es.wikipedia.org/wiki/Archivo:Refracci%C3%B3n.svg
En 1967 el físico-matemático ruso Viktor Veselago, del Instituto de Física de Moscú, trabajaba con las propiedades fundamentales de la materia que determinan la propagación de las ondas electromagnéticas en su interior: la constante dieléctrica (Ɛ) y la permeabilidad magnética (µ). Él predijo que si no se tomaba en cuenta la pérdida de energía que sufre la radiación al propagarse por el medio, ambas variables podían cambiar simultáneamente de signo (Ɛ<0, µ<0) sin afectar las propiedades elementales de la sustancia, sin embargo, su índice de refracción adquiriría también un valor negativo; aceptó que eso contradecía las leyes de la naturaleza y que no existía en ella ningún material con tales características ni se disponía de la tecnología para crearlo (Fig. 2 y 3)3
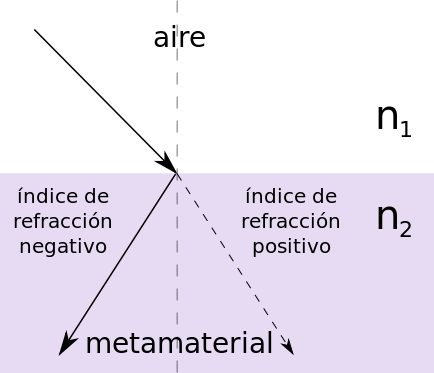
Figura 2. Cuando la constante dieléctrica y la permeabilidad magnética de un material tienen valores negativos el ángulo de refracción es negativo. Imagen tomada de: https://es.m.wikipedia.org/wiki/Archivo:Refracci%C3%B3n_negativa.svg

Figura 3. Cuando la luz entra a un medio de diferente densidad es desviada por sus moléculas, dando la impresión de que el objeto se dobla. Si el agua tuviera índice de refracción negativo el objeto parecería doblarse hacia el lado opuesto. Imagen tomada de: https://commons.wikimedia.org/wiki/File:Metamaterial.jpg
Sin embargo, en el año 2000, el físico teórico John Pendry, del Colegio Imperial de Londres, profundizó en la teoría de Veselago y, echando mano de la nanotecnología, desarrolló un superlente hecho de filamentos de plata y anillos resonadores de un tamaño menor a la longitud de onda de la luz visible. Ver Figura 4. Este metamaterial, a diferencia de los materiales convencionales, no está limitado por su composición sino por su arreglo ultraestructural, de aquí se desprenden cambios en las propiedades básicas de las lentes.4

Figura 4. Organización estructural de un metamaterial.
Imagen tomada de: https://i.kinja-img.com/gawker-media/image/upload/c_fill,f_auto,fl_progressive,g_center,h_675,pg_1,q_80,w_1200/18dxmf4szsfe6jpg.jpg
En primer lugar, su índice de refracción resulta negativo (-n); aunque la Ley de Snell se mantiene vigente y el rayo refractado se aproxima a la línea normal perpendicular a la superficie, el signo del ángulo de refracción es negativo, en consecuencia, un lente convexo hace divergir la luz y un lente cóncavo le hace converger. Un concepto opuesto a lo que estamos acostumbrados.5
Otro fenómeno exótico de los metamateriales se relaciona al efecto Doppler de la luz. En el sonido, la frecuencia aparente de una onda sonora cambia al alejarse o acercarse la fuente emisora a la persona que escucha, alterando el tono del sonido; en la luz el principio es semejante pero el cambio se produce en el color, principalmente hacia las frecuencias altas; para un observador el color de una montaña es azul si está lejos de ella o bien verde si se aproxima. En condiciones normales la luz se disipa al alejarse de la fuente, este efecto de evanescencia no se presenta al viajar a través de un metamaterial, de hecho, lejos de evanecer, la señal se amplifica a través de él. Sustituyendo las lentes comunes del más sencillo microscopio óptico por superlentes modeladas digitalmente podría observarse incluso la estructura helicoidal del ADN; la microscopía electrónica pronto pasará a ser el juguete con el que se divertirán los niños.5
El instrumento óptico más simple es una perforación en una pantalla plástica opaca. Parte de la luz que incide la atraviesa y el resto se absorbe o refleja. Sí el diámetro del agujero mantiene un tamaño mayor a la longitud de onda de la luz (d>λ) las ondas que lo atraviesan difractan, pero el ángulo de salida será igual al de entrada; si el agujero no supera en tamaño a la longitud de onda (d<λ), la transmisión de luz será baja y además irradiará isotrópicamente, es decir, se distribuirá por igual en todas direcciones, limitando su capacidad de conducción en espacios pequeños. En cambio, si la pantalla opaca se reemplaza por una metálica y se le hace una serie de pequeños agujeros -del orden de 280nm- la luz interactuará con los electrones superficiales del material -plasmones- y será transportada bidimensionalmente hacia los orificios aumentando su transmisión.6
Con los nuevos metamateriales de refracción negativa aparece una nueva familia de plasmones superficiales capaces de propagar la luz mucho mejor que cualquier fibra óptica y a cualquier distancia sin necesidad de repetidores que amplifiquen la señal cuando esta cae ni el inconveniente de la reflexión total interna. No solo eso, la luz también podría ser comprimida y almacenada como se hace con un archivo digital eliminando la necesidad de circuitos electrónicos y reemplazándolos por circuitos fotónicos más pequeños y poderosos.1

Héctor Esparza. OD
REFERENCIAS
- Depine R, Exactas C, Aires B. Los metamateriales. Luz obediente. Fac ciencias Nat y exactas Univ Buenos Aires [Internet]. Available from: http:// www.fcen.uba.ar/fotovideo/EXm/NotasEXm48/ exm48metamateriales.pdf
2. Tippens PE. Física. Conceptos y aplicaciones. 7th ed. USA: McGraw-Hill Education; 2011.
3. Veselago VG. The Electrodynamic of Substances with Simultaneous Negative Values of e and µ. Sov Phys Uspekhi. 1968;10(4):509–14.
4. Pendry JB. Negative refraction makes a perfect lens. Phys Rev Lett. 2000;85(18):3966–9. 5. Rudko GY. Novel concepts of negative-n optics in master’s level educational courses. Semicond Phys Quantum Electron Optoelectron. 2017;20(2):235–9. 6. García Vidal F, Martínez Moreno L. Plasmones superficiales. Investig Cienc. 2008;(385):66–76.
.
.






Muy interesante esto va a revolucionar los conceptos de óptica.